浅谈状态压缩
总览
状态压缩是什么
别名“二进制枚举”,核心是枚举。即将所有的情况枚举出来后对每种情况进行单独的讨论。对于每一个下标我将其称作 “非黑即白”(在某一情况中要么出现要么不出现)。
可以将其看作对数据范围小的布尔数组的压缩。但由于有位运算,使状态压缩操作起来比布尔数组简洁。(状态压缩能做的事情布尔数组都能做、只是写起来繁琐)
为什么能用状态压缩
这得从$C$语言的底层说起,一个int型的变量有$4$个字节、即$32$位bit。每一位bit只能由$0$或$1$组成、可以将其看作布尔数组。
#include <bits/stdc++.h>
using namespace std;
int main()
{
int a = 1;
printf("int的字节: %d\n", sizeof(a));
a <<= 31;
printf("最右边的1移到了符号位,将输出int的最小值: %d\n", a);
a = 1; a <<= 1;
printf("此时只左移了一位,将以十进制输出二进制的10: %d\n", a);
return 0;
}什么情况下用状态压缩
通常情况下数据范围$25$以内且需要枚举的可以使用状态压缩
状态压缩怎么用
先确定枚举数组的长度,利用二进制数字做加法时不重不漏的特性将所有情况枚举出来,再依据题意处理每一个情况。
例题
例一、子集
https://leetcode-cn.com/problems/subsets/
题目
给你一个整数数组 $nums$,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0]
输出:[[],[0]]提示:
1 <= nums.length <= 10
-10 <= nums[i] <= 10
nums 中的所有元素 互不相同思路分析
每一个下标只有两种可能:被选或不被选,将这些情况组合到一起就是答案了。时间是$2^{10}$,计算结果为1024,完全可行。
解法一、dfs
于是在知道状态压缩之前最直观的想法就是$dfs$了。
class Solution {
public:
int n;
vector<bool> b; //核心数据结构
vector<vector<int>> ans;
vector<vector<int>> subsets(vector<int>& nums) {
n = nums.size();
b.resize(n);
dfs(0, nums);
return ans;
}
//核心算法
void dfs(int u, vector<int>& nums)
{
//结束条件
if(u == n)
{
vector<int> tmp;
for(int i = 0; i < n; ++ i) if(b[i]) tmp.push_back(nums[i]);
ans.push_back(tmp);
return ;
}
//每个下标要么被选要么不被选
b[u] = true;
dfs(u + 1, nums); //被选上
b[u] = false;
dfs(u + 1, nums); //不被选上
}
};解法二、状态压缩
仔细观察$dfs$中用到的布尔数组:它的最大长度是$10$;每个位置不是$false$就是$true$。再观察$dfs$算法:将所有的情况都枚举出来。这些特性满足状态压缩的使用条件。下面给出状态压缩的写法
class Solution {
public:
vector<vector<int>> subsets(vector<int>& nums) {
vector<vector<int>> ans;
int n = nums.size();
for(int i = 0; i < 1 << n; ++ i)
{
//每个i对应一种情况
vector<int> tmp;
//最多只有n位有效的数字
for(int j = 0; j < n; ++ j)
if((i >> j) & 1) //第j位在当前的枚举情况下被选上了
tmp.push_back(nums[j]);
ans.push_back(tmp);
}
return ans;
}
};例二、两个回文子序列长度的最大乘积
https://leetcode-cn.com/problems/maximum-product-of-the-length-of-two-palindromic-subsequences/
题目
给你一个字符串 $s$ ,请你找到 $s$ 中两个 不相交回文子序列 ,使得它们长度的 乘积最大 。两个子序列在原字符串中如果没有任何相同下标的字符,则它们是 不相交 的。
请你返回两个回文子序列长度可以达到的 最大乘积 。
子序列 指的是从原字符串中删除若干个字符(可以一个也不删除)后,剩余字符不改变顺序而得到的结果。如果一个字符串从前往后读和从后往前读一模一样,那么这个字符串是一个 回文字符串 。
示例 1:
输入:s = "leetcodecom"
输出:9
解释:最优方案是选择 "ete" 作为第一个子序列,"cdc" 作为第二个子序列。
它们的乘积为 3 * 3 = 9 。
示例 2:
输入:s = "bb"
输出:1
解释:最优方案为选择 "b" (第一个字符)作为第一个子序列,"b" (第二个字符)作为第二个子序列。
它们的乘积为 1 * 1 = 1 。
示例 3:
输入:s = "accbcaxxcxx"
输出:25
解释:最优方案为选择 "accca" 作为第一个子序列,"xxcxx" 作为第二个子序列。
它们的乘积为 5 * 5 = 25 。示例一的图解:
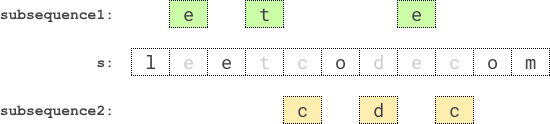
提示:
2 <= s.length <= 12
s 只含有小写英文字母。思路分析
数据范围只有$12$。将所有子序列枚举出来的时间复杂度是$2^{n^2}$,判断回文的时间复杂度是$O(n)$。找到所有回文的时间复杂度为$n 2^{n^2}$,判断最大长度为$O(1)$,总的时间复杂度为$n 2^{n^2}$,将12带入计算得$201326592$,时间是$2 * 10^8$,但是很可能$TLE$,不过可以用状态压缩试试。
代码 暴力状态压缩 用时1808ms
class Solution {
public:
int maxProduct(string s) {
vector<int> a; //存是回文的长度
int n = s.size();
int maxn = 1;
//不重不漏地枚举出所有情况
for(int i = 0; i < (1 << n) - 1; ++ i)
{
for(int j = i + 1; j < (1 << n) - 1; ++ j)
{
if(i & j) continue; //有交集
string x, y;
for(int k = 0; k < n; ++ k) if(i >> k & 1) x += s[k];
for(int k = 0; k < n; ++ k) if(j >> k & 1) y += s[k];
if(check(x) && check(y)) maxn = max(maxn, count(i) * count(j)); //更新答案
}
}
return maxn;
}
//判断u是不是回文序列
bool check(string u)
{
string x = u;
reverse(u.begin(), u.end());
return x == u;
}
//计算x的二进制表示中1的个数
int count(int x)
{
int ans = 0;
while(x)
{
x &= (x - 1); //每次去掉最右边的1
ans ++;
}
return ans;
}
};例三、猜字谜
https://leetcode-cn.com/problems/number-of-valid-words-for-each-puzzle/
题目
外国友人仿照中国字谜设计了一个英文版猜字谜小游戏,请你来猜猜看吧。
字谜的迷面 $puzzle$ 按字符串形式给出,如果一个单词 $word$ 符合下面两个条件,那么它就可以算作谜底:
单词 word 中包含谜面 puzzle 的第一个字母。
单词 word 中的每一个字母都可以在谜面 puzzle 中找到。
例如,如果字谜的谜面是 "abcdefg",那么可以作为谜底的单词有 "faced", "cabbage", 和 "baggage";而 "beefed"(不含字母 "a")以及 "based"(其中的 "s" 没有出现在谜面中)都不能作为谜底。返回一个答案数组 $answer$,数组中的每个元素 $answer[i] $是在给出的单词列表 $words$ 中可以作为字谜迷面 $puzzles[i]$ 所对应的谜底的单词数目。
示例:
输入:
words = ["aaaa","asas","able","ability","actt","actor","access"],
puzzles = ["aboveyz","abrodyz","abslute","absoryz","actresz","gaswxyz"]
输出:[1,1,3,2,4,0]
解释:
1 个单词可以作为 "aboveyz" 的谜底 : "aaaa"
1 个单词可以作为 "abrodyz" 的谜底 : "aaaa"
3 个单词可以作为 "abslute" 的谜底 : "aaaa", "asas", "able"
2 个单词可以作为 "absoryz" 的谜底 : "aaaa", "asas"
4 个单词可以作为 "actresz" 的谜底 : "aaaa", "asas", "actt", "access"
没有单词可以作为 "gaswxyz" 的谜底,因为列表中的单词都不含字母 'g'。提示:
1 <= words.length <= 10^5
4 <= words[i].length <= 50
1 <= puzzles.length <= 10^4
puzzles[i].length == 7
words[i][j], puzzles[i][j] 都是小写英文字母。
每个 puzzles[i] 所包含的字符都不重复。思路分析
注意到 words[i][j], puzzles[i][j] 都是小写英文字母,小写字母有多少个?$26$个。在$int32$的范围内,不如这样:将每个单词都变成一个$int$数字,数字的每一个$bit$记录该单词中有没有出现特定的字母。
由数据范围可知大概率不能直接双重循环、因为直接循环的时间复杂度高达$10^9$,几乎一定超时。题目只要求算出次数、想到用哈希表存放特定数字出现的次数。注意到puzzles[i]的长度为$7$,它的所有可能为$2^7 == 128$,符合要求的words[i]二进制表示中$1$的次数不能超过$2^7$,大大减少了枚举量。
将两个数组的二进制算出来用时$26 (10^5 + 10^4)$,双重枚举用时$2^{7^2}$,两个相加约为$3 10^6$,再算上哈希表(最多只有$128$种可能)查找插入时的时间开销、总和一定小于$10^8$,理论上是可行的。
代码
class Solution {
public:
// 计算二进制表示中1的个数
int count(int x)
{
int ans = 0;
while(x)
{
ans ++;
x &= (x - 1);
}
return ans;
}
vector<int> findNumOfValidWords(vector<string>& words, vector<string>& puzzles) {
int n = words.size(), m = puzzles.size();
unordered_map<int, int> m1; //用来存次数的哈希表
vector<int> ans;
//初始化m1
for(auto &i : words)
{
int tmp = 0;
for(auto &j : i) tmp |= (1 << (j - 'a'));
if(count(tmp) > 7) continue; //1小于等于7次才有可能成为谜底
m1[tmp] ++;
}
//对于每个pu 遍历所有的哈希表
for(auto &i : puzzles)
{
int tmp = 0;
for(auto &j : i) tmp |= (1 << (j - 'a'));
int p = 0;
//每个谜面都暴力枚举一次哈希表
for(auto &[x, y] : m1)
{
//一定要注意优先级啊!!特别是后面的((x | tmp) == tmp)
//要求x是tmp的子集,x | tmp没有扩容就说明x是tmp的子集
if( ((x >> (i[0] - 'a')) & 1) && ((x | tmp) == tmp))
p += y;
}
ans.push_back(p);
}
return ans;
}
};例四、得分最高的单词集合
https://leetcode-cn.com/problems/maximum-score-words-formed-by-letters/
题目
你将会得到一份单词表 $words$,一个字母表$letters$(可能会有重复字母),以及每个字母对应的得分情况表$score$。
请你帮忙计算玩家在单词拼写游戏中所能获得的「最高得分」:能够由 $letters$ 里的字母拼写出的 任意 属于 $words$ 单词子集中,分数最高的单词集合的得分。
单词拼写游戏的规则概述如下:
玩家需要用字母表 letters 里的字母来拼写单词表 words 中的单词。
可以只使用字母表 letters 中的部分字母,但是每个字母最多被使用一次。
单词表 words 中每个单词只能计分(使用)一次。
根据字母得分情况表score,字母 'a', 'b', 'c', ... , 'z' 对应的得分分别为 score[0], score[1], ..., score[25]。
本场游戏的「得分」是指:玩家所拼写出的单词集合里包含的所有字母的得分之和。示例 1:
输入:words = ["dog","cat","dad","good"], letters = ["a","a","c","d","d","d","g","o","o"], score = [1,0,9,5,0,0,3,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,0,0,0]
输出:23
解释:
字母得分为 a=1, c=9, d=5, g=3, o=2
使用给定的字母表 letters,我们可以拼写单词 "dad" (5+1+5)和 "good" (3+2+2+5),得分为 23 。
而单词 "dad" 和 "dog" 只能得到 21 分。
示例 2:
输入:words = ["xxxz","ax","bx","cx"], letters = ["z","a","b","c","x","x","x"], score = [4,4,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,5,0,10]
输出:27
解释:
字母得分为 a=4, b=4, c=4, x=5, z=10
使用给定的字母表 letters,我们可以组成单词 "ax" (4+5), "bx" (4+5) 和 "cx" (4+5) ,总得分为 27 。
单词 "xxxz" 的得分仅为 25 。
示例 3:
输入:words = ["leetcode"], letters = ["l","e","t","c","o","d"], score = [0,0,1,1,1,0,0,0,0,0,0,1,0,0,1,0,0,0,0,1,0,0,0,0,0,0]
输出:0
解释:
字母 "e" 在字母表 letters 中只出现了一次,所以无法组成单词表 words 中的单词。提示:
1 <= words.length <= 14
1 <= words[i].length <= 15
1 <= letters.length <= 100
letters[i].length == 1
score.length == 26
0 <= score[i] <= 10
words[i] 和 letters[i] 只包含小写的英文字母。思路分析
words的长度只有$14$,可以枚举所有情况后对每一种情况做单独判断:满足可以被拼出来时更新答案。
先将letters中字母出现的次数存入哈希表,用时不到$100$。枚举所有情况的时间为$2^{14} = 16384$,每种情况下对哈希表查找$15$次、更新答案算$15$次,总用时在$3 * 10^5$之下。暴力可行。
代码
class Solution {
public:
int maxScoreWords(vector<string>& words, vector<char>& letters, vector<int>& score) {
int n = words.size();
int a[26] = {0}, b[26], maxn = 0, tmp = 0;
for(auto &i : letters) a[i - 'a'] ++; //存放所有字母出现过的次数
for(int i = 0; i < 1 << n; i ++)
{
memcpy(b, a, sizeof a);
tmp = 0;
//枚举所有的情况
for(int j = 0; j < n; ++ j)
//第j个在情况里面
if(i >> j & 1)
for(auto &t : words[j])
b[t - 'a'] --, tmp += score[t - 'a'];
//判断该情况是否可行(会不会将字母用超)
for(auto &j : b) if(j < 0) goto g;
maxn = max(maxn, tmp);
g:;
}
return maxn;
}
};例五、最多可达成的换楼请求数目
https://leetcode-cn.com/problems/maximum-number-of-achievable-transfer-requests/
题目
我们有 $n$ 栋楼,编号从 $0$ 到 $n - 1$ 。每栋楼有若干员工。由于现在是换楼的季节,部分员工想要换一栋楼居住。
给你一个数组 $requests$ ,其中 $requests[i] = [fromi, toi]$ ,表示一个员工请求从编号为 $fromi$的楼搬到编号为$toi$ 的楼。
一开始 所有楼都是满的,所以从请求列表中选出的若干个请求是可行的需要满足 每栋楼员工净变化为 $0$ 。意思是每栋楼 离开 的员工数目 等于 该楼 搬入 的员工数数目。比方说 $n = 3$且两个员工要离开楼$0$ ,一个员工要离开楼 $1$,一个员工要离开楼 $2$ ,如果该请求列表可行,应该要有两个员工搬入楼$0$ ,一个员工搬入楼$1$ ,一个员工搬入楼$2$ 。
请你从原请求列表中选出若干个请求,使得它们是一个可行的请求列表,并返回所有可行列表中最大请求数目。
示例 1:
输入:n = 5, requests = [[0,1],[1,0],[0,1],[1,2],[2,0],[3,4]]
输出:5
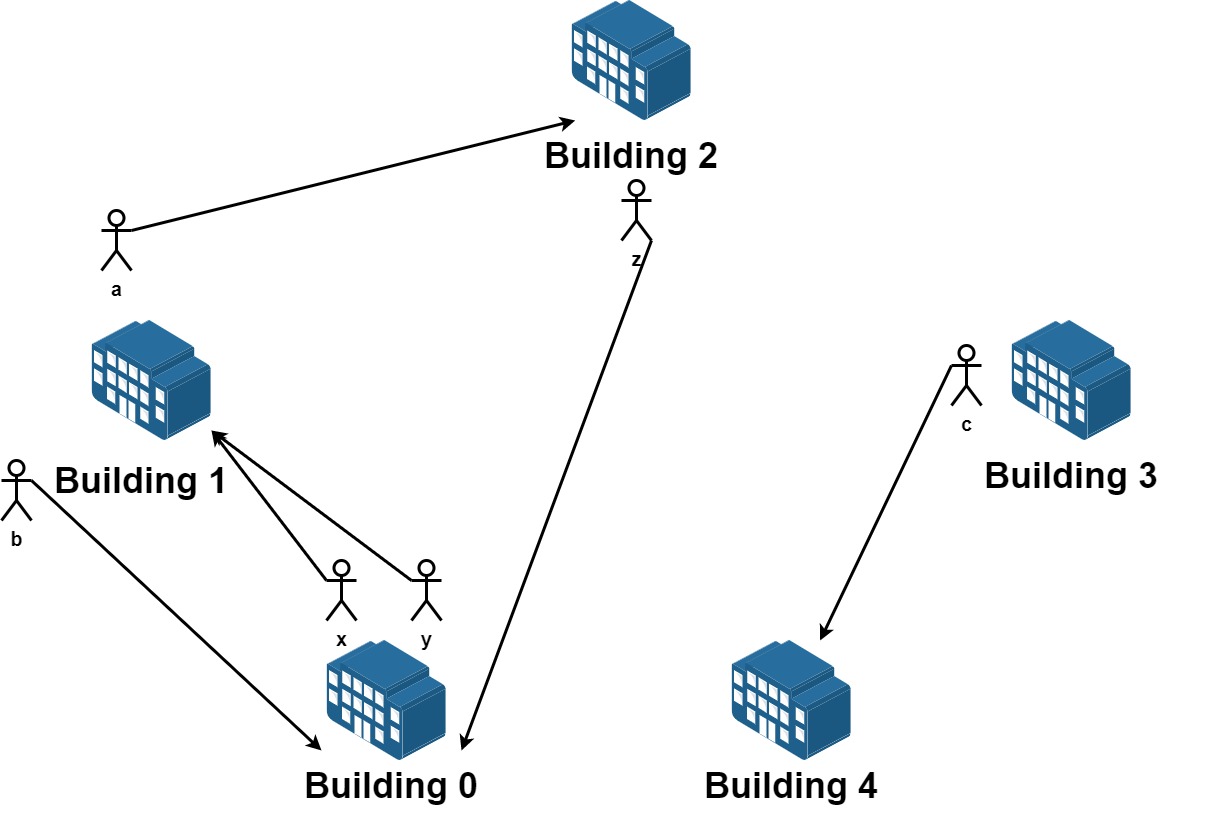
解释:请求列表如下:
从楼 0 离开的员工为 x 和 y ,且他们都想要搬到楼 1 。
从楼 1 离开的员工为 a 和 b ,且他们分别想要搬到楼 2 和 0 。
从楼 2 离开的员工为 z ,且他想要搬到楼 0 。
从楼 3 离开的员工为 c ,且他想要搬到楼 4 。
没有员工从楼 4 离开。
我们可以让 x 和 b 交换他们的楼,以满足他们的请求。
我们可以让 y,a 和 z 三人在三栋楼间交换位置,满足他们的要求。
所以最多可以满足 5 个请求。示例一图解
示例 2:
输入:n = 3, requests = [[0,0],[1,2],[2,1]]
输出:3
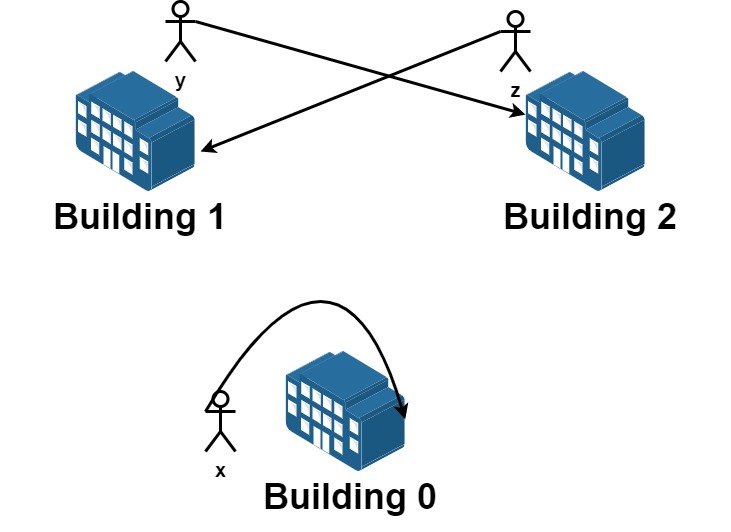
解释:请求列表如下:
从楼 0 离开的员工为 x ,且他想要回到原来的楼 0 。
从楼 1 离开的员工为 y ,且他想要搬到楼 2 。
从楼 2 离开的员工为 z ,且他想要搬到楼 1 。
我们可以满足所有的请求。示例二图解
示例 3:
输入:n = 4, requests = [[0,3],[3,1],[1,2],[2,0]]
输出:4提示:
1 <= n <= 20
1 <= requests.length <= 16
requests[i].length == 2
0 <= fromi, toi < n思路分析
注意到数据范围只有$20$,将所有情况枚举出来后对于每个情况而言无非是每个节点的入度要等于出度。
总的时间约为$2^{20} 16 2 = 2 * 10^6$。
代码
class Solution {
public:
//计算出二进制中1的个数
int count(int x)
{
int ans = 0;
while(x) ans ++, x &= (x - 1);
return ans;
}
int maximumRequests(int n, vector<vector<int>>& requests) {
int maxn = 0;
int a[n]; //记录每个节点的出入度情况 入度+1 出度-1
int m = requests.size();
//枚举所有情况
for(int i = 0; i < 1 << m; ++ i)
{
memset(a, 0, sizeof a);
for(int j = 0; j < m; ++ j)
if(i >> j & 1)
a[requests[j][0]] --, a[requests[j][1]] ++;
for(auto &j : a) if(j) goto g; //不能满足入度等于出度的话就排除该假设
maxn = max(maxn, count(i));
g:;
}
return maxn;
}
};例六、基于陈述统计最多好人数
https://leetcode-cn.com/problems/maximum-good-people-based-on-statements/
题目
游戏中存在两种角色:
好人:该角色只说真话。
坏人:该角色可能说真话,也可能说假话。给你一个下标从 0 开始的二维整数数组 $statements$ ,大小为 $n * n$ ,表示$ n $个玩家对彼此角色的陈述。具体来说,$statements[i][j] $可以是下述值之一:
0 表示 i 的陈述认为 j 是 坏人 。
1 表示 i 的陈述认为 j 是 好人 。
2 表示 i 没有对 j 作出陈述。另外,玩家不会对自己进行陈述。形式上,对所有$0 <= i < n$,都有$statements[i][i] = 2$ 。
根据这 $n$ 个玩家的陈述,返回可以认为是 好人 的 最大 数目。
示例 $1$:

输入:statements = [[2,1,2],[1,2,2],[2,0,2]]
输出:2
解释:每个人都做一条陈述。
- 0 认为 1 是好人。
- 1 认为 0 是好人。
- 2 认为 1 是坏人。
以 2 为突破点。
- 假设 2 是一个好人:
- 基于 2 的陈述,1 是坏人。
- 那么可以确认 1 是坏人,2 是好人。
- 基于 1 的陈述,由于 1 是坏人,那么他在陈述时可能:
- 说真话。在这种情况下会出现矛盾,所以假设无效。
- 说假话。在这种情况下,0 也是坏人并且在陈述时说假话。
- 在认为 2 是好人的情况下,这组玩家中只有一个好人。
- 假设 2 是一个坏人:
- 基于 2 的陈述,由于 2 是坏人,那么他在陈述时可能:
- 说真话。在这种情况下,0 和 1 都是坏人。
- 在认为 2 是坏人但说真话的情况下,这组玩家中没有一个好人。
- 说假话。在这种情况下,1 是好人。
- 由于 1 是好人,0 也是好人。
- 在认为 2 是坏人且说假话的情况下,这组玩家中有两个好人。
在最佳情况下,至多有两个好人,所以返回 2 。
注意,能得到此结论的方法不止一种。示例 $2$:
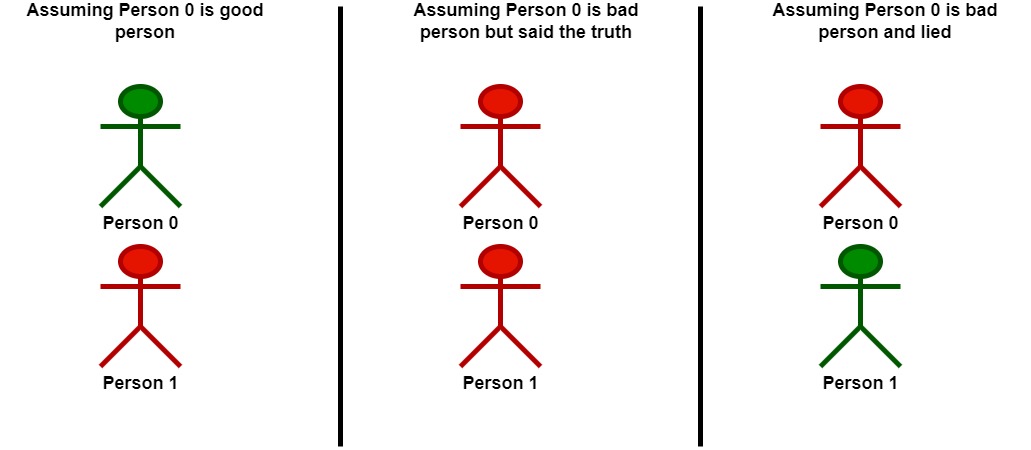
输入:statements = [[2,0],[0,2]]
输出:1
解释:每个人都做一条陈述。
- 0 认为 1 是坏人。
- 1 认为 0 是坏人。
以 0 为突破点。
- 假设 0 是一个好人:
- 基于与 0 的陈述,1 是坏人并说假话。
- 在认为 0 是好人的情况下,这组玩家中只有一个好人。
- 假设 0 是一个坏人:
- 基于 0 的陈述,由于 0 是坏人,那么他在陈述时可能:
- 说真话。在这种情况下,0 和 1 都是坏人。
- 在认为 0 是坏人但说真话的情况下,这组玩家中没有一个好人。
- 说假话。在这种情况下,1 是好人。
- 在认为 0 是坏人且说假话的情况下,这组玩家中只有一个好人。
在最佳情况下,至多有一个好人,所以返回 1 。
注意,能得到此结论的方法不止一种。思路分析
数据范围只有15,枚举所有情况的时间为$2^{15}$,验证每种情况的合理性的时间为$15^2$,总时间为$2^{15} * 15^2$,即$7372800$,在$10^8$以内。
代码
class Solution {
public:
int maximumGood(vector<vector<int>>& statements) {
int n = statements.size(), maxn = 0;
//枚举所有情况
for(int i = 0; i < 1 << n; ++ i)
{
for(int j = 0; j < n; ++ j)
{
//第j个人是好人
if(i >> j & 1)
{
for(int k = 0; k < n; ++ k)
{
if(statements[j][k] == 2) continue;
//如果陈述不同则该情况为错
if(statements[j][k] ^ (i >> k & 1) == 1) goto g;
}
}
}
maxn = max(maxn, count(i));
g:;
}
return maxn;
}
//计算x的二进制表示中有几个1
int count(int x)
{
int ans = 0;
while(x)
{
x &= (x - 1); //去掉最右边的1
ans ++;
}
return ans;
}
};总结
- 状态压缩实质上是布尔数组
for(int i = 0; i < 1 << n; ++ i)布尔数组的长度是$n$,从全$0$到全$1$,不重不漏地枚举出来了i >> j & 1判断第$j$位的状态- 注意数据范围。如例三、通过哈希表将$10^5$和$10^4$改成$2^7$和$2^7$
状态压缩大致模板
for(int i = 0; i < 1 << n; ++ i)
{
//每个i是一种情况
for(int j = 0; j < n; ++ j)
{
//对当前情况下的每一位检查
if(i >> j & 1)
{
//依题意
}
}
}计算某个数字的二进制表示中$1$的数量
int count(int x)
{
int ans = 0;
while(x) ans ++, x &= (x - 1); //去掉最右边的1
return ans;
}