前言
这篇文章用三道例题解释下单调栈
单调栈是什么
栈里的元素 严格或非严格 单调递增或递减
实现时要维护栈内的元素有序
例题一 Acwing1978(简单)
题目链接 https://www.acwing.com/problem/content/description/1980/
题目
每天,农夫约翰的 N头奶牛都会穿过农场中间的马路。考虑约翰的农场在二维平面的地图,马路沿水平方向延伸,马路的一侧由直线 y=0描述,另一侧由直线 y=1描述。奶牛 i从马路一侧的位置 (ai,0) 沿直线过马路到达另一侧的位置 (bi,1)。
所有 ai互不相同,所有 bi互不相同。
尽管他的奶牛们行动敏捷,他还是担心行动路径交叉的两头奶牛在过马路时发生碰撞。
约翰认为,如果一头奶牛的行动路径没有跟其他任何奶牛的行动路径相交,则该奶牛是安全的。
请帮助约翰计算安全奶牛的数量。
输入格式
第一行包含整数 N。
接下来 N行,每行包含两个整数 ai,bi,用来描述一头牛的行动路径。
输出格式
输出安全奶牛的数量。
数据范围
$1≤N≤10^5,−10^6≤a_i,b_i≤10^6$
输入样例
4
-3 4
7 8
10 16
3 9输出样例
2样例解释
第一头牛和第三头牛的行动路线不与其他奶牛的路线相交。
第二头牛和第四头牛的行动路线相交。
题目分析
排序必不可少、之后用到了单调栈(严格单调递增栈)的算法:
- 新加的元素如果比最大值大、它一定可以被加进来
- 新加的元素如果比最大值小、有可能出现交集的情况、通过删除栈内元素维持栈的单调递增的特性
代码
#include <bits/stdc++.h>
using namespace std;
struct Node
{
int x;
int y;
};
bool cmp(Node &p1, Node &p2)
{
return p1.x < p2.x;
}
int main()
{
int n; cin >> n;
Node a[n];
for (int i = 0; i < n; i ++ ) scanf("%d%d", &a[i].x, &a[i].y);
sort(a, a + n, cmp); //按x从小到大排序、进栈元素为y
stack<int> sta; //单调严格递增栈
int maxn = -1e7;
for(int i = 0; i < n; ++ i)
{
if(maxn < a[i].y) sta.push(a[i].y); //新进来的不会和原来的有交集
else
while(sta.size() && sta.top() > a[i].y) //不然可能有交集、将相交的部分全部清空
sta.pop();
maxn = max(maxn, a[i].y); //每次更新下最大值
}
cout << sta.size();
return 0;
}例题二 力扣402(中等)
题目链接 https://leetcode-cn.com/problems/remove-k-digits/
题目
给你一个以字符串表示的非负整数 num 和一个整数 k ,移除这个数中的 k 位数字,使得剩下的数字最小。请你以字符串形式返回这个最小的数字。
示例 1 :
输入:num = "1432219", k = 3
输出:"1219"
解释:移除掉三个数字 4, 3, 和 2 形成一个新的最小的数字 1219 。
示例 2 :
输入:num = "10200", k = 1
输出:"200"
解释:移掉首位的 1 剩下的数字为 200. 注意输出不能有任何前导零。
示例 3 :
输入:num = "10", k = 2
输出:"0"
解释:从原数字移除所有的数字,剩余为空就是 0 。
提示:
1 <= k <= num.length <= 105
num 仅由若干位数字(0 - 9)组成
除了 0 本身之外,num 不含任何前导零题目分析
一个直观的思路就是将出现在前面且大的数字删掉。是一个单调栈思想。将字符串的右边看作栈的开口,字符串左边封闭。
围绕这个核心完善细节:
- 每预加一个数时将它前面出现的比它大的删去、删一个减一次总次数
- 有前导零的情况:清空
- 最后遍历一遍后任可能总次数未被减到0,从后往前删除
- 最后如果为空返回0
代码
class Solution {
public:
string removeKdigits(string num, int k) {
//升序
int n = num.size();
string s; //将字符串抽象成栈,左边是栈底、右边是带有开口的栈顶
for(int i = 0; i < n; ++ i)
{
//核心思想就是将出现在前面的大的数删去
while(k && s.size() && s.back() > num[i]) s.pop_back(), k --; //每次减总次数
if(s == "0") s = ""; //去除前缀0
s.push_back(num[i]); //将当前加入答案
}
while(k && s.size()) s.pop_back(), k--; //此时的栈是一个非严格单调递增、从后往前删
if(!s.size()) return "0"; //特判
return s;
}
};例题三 力扣84(困难)
题目链接 https://leetcode-cn.com/problems/largest-rectangle-in-histogram/
题目
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
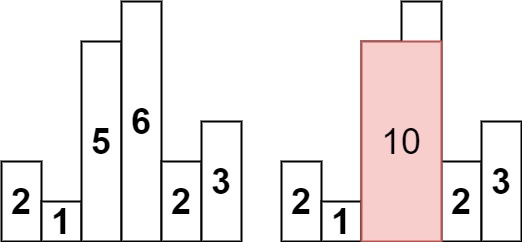
输入:heights = [2,1,5,6,2,3]
输出:10
解释:最大的矩形为图中红色区域,面积为 10数据范围
- $ 1 <= heights.length <=10^5 $
- $0 <= heights[i] <= 10^4$
题目分析
暴力做法是枚举每一个点、将这个点向两边双指针遍历、遇到小于它的元素时终止双指针遍历。但是在极端情况下该做法的时间复杂度高达$O(n^2)$ ,是个效率堪忧的算法。
栈的特点是什么?先进后出。从左到右遍历的过程中每个可能的点向左寻找答案,符合栈的特性。
核心思想是向右遍历过程中维护一个非严格单调递增栈,当不能确定答案时将下标入栈、能够确定答案时将所有不必要数据出栈。
一些细节:
-
栈只用存下标
-
最后要拟入栈一个比所有数小的数字将栈清空
-
带有一点点贪心策略:如原栈是$134$,拟入栈$2$,$3$和$4$在之后高度最高只能到$2$了,要更新下原数组的高度
代码
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
heights.push_back(-1); //确保在最后将栈清空
int n = heights.size();
stack<int> sta;
int ans = 0, tmp;
for(int i = 0; i < n; ++ i)
{
if(sta.empty() || heights[i] >= heights[sta.top()]) sta.push(i); //不能确定答案、先入栈
else // 能确定答案了
{
int idx;
while(sta.size() && heights[i] < heights[sta.top()]) //维护栈的非严格单调递增
{
idx = sta.top();
sta.pop();
ans = max(ans, heights[idx] * (i - idx)); //更新答案
}
sta.push(idx); //将拟入栈的入栈
heights[idx] = heights[i]; //改变原数组的数据大小,只能这么高了
}
}
return ans;
}
};总结
单调栈的核心是维护栈内数据有序。在满足有序的前提下直接入栈;不满足的话通过删除栈内数据达到有序。
伪代码大致是:
for(int i = 0; i < n; ++ i) //从左到右遍历一遍
{
if(sta.empty() || f1) sta.push(i); //直接入栈 f1是满足某条件
else //不然的话维护栈内元素有序
{
while(sta.size() && f2) //只要不能有序就一直删
{
sta.pop(); //通过删除来满足栈内有序
x1; //执行的其它语句
}
}
x2; //根据题目要求写
}