配套视频：https://www.bilibili.com/video/BV1Su41197rq?spm_id_from=333.999.0.0

模板

BFS有强烈的“步数”意识。每一步的搜索向外扩展一层。

BFS的核心是搜索：让每个点向所有可能的方向搜索。

核心模板如下（带注释）

while(q.size())
{
    int len = q.size();
    //依据题意总步数或其他
    while(len --)
    {
        auto [x, y] = q.front(); q.pop();
        //尝试向外拓展
        for(int i = 0; i < 方向总数; ++ i)
        {
            int xx = x + dx[i], yy = y + dy[i];
            //即将搜索的坐标越界或已经被搜索过
            if(xx < 0 || xx >= n || yy < 0 || yy >= m || b[xx][yy]) continue; 
            q.push({xx, yy}); b[xx][yy] = 1;
        }
    }
}

一、单源

例一、岛屿的最大面积

链接：https://leetcode-cn.com/problems/max-area-of-island/

题目

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

示例 1：

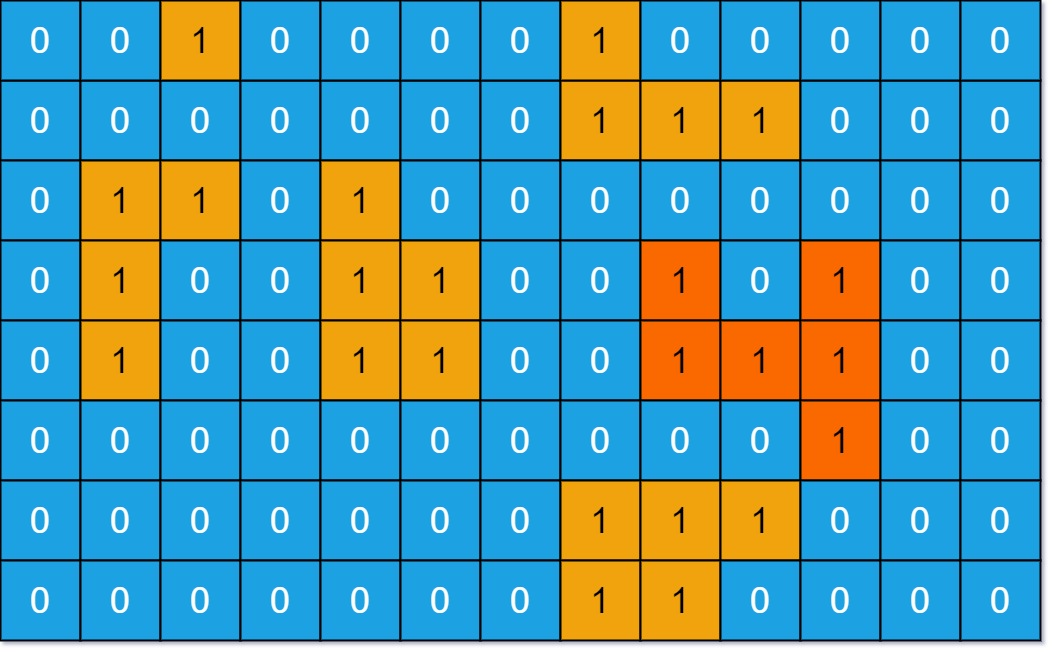
输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

示例 2：

输入：grid = [[0,0,0,0,0,0,0,0]]
输出：0

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 50
grid[i][j] 为 0 或 1

题目分析

经典的单源bfs。每个点的搜索方向只有$4$个

遍历一遍二维矩阵，某个点为$1$且未被访问过就从该点出发搜索。

参考代码（带注释）

class Solution {
public:
    int dx[4] = {0,0,1,-1}; int dy[4] = {1,-1,0,0}; //搜索的四个方向
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();
        int maxn = 0;
        vector<vector<bool>> b(n, vector<bool>(m)); //布尔数组标记有没有被访问
        for(int i = 0; i < n; ++ i)
        {
            for(int j = 0; j < m; ++ j)
            {
                if(b[i][j]) continue;
                b[i][j] = true;
                if(!grid[i][j]) continue; //该点即未被访问又为1 那就从这个点开始搜索
                queue<pair<int, int>> q;
                q.push({i, j});
                int tmp = 0;
                while(q.size())
                {
                    int len = q.size();
                    tmp += len; //记录一个"1连接块"中"1"的个数
                    for(int k = 0; k < len; ++ k)
                    {
                        auto [x, y] = q.front();
                        q.pop();
                        for(int t = 0; t < 4; ++ t)
                        {
                            int xx = x + dx[t], yy = y + dy[t];
                            if(xx < 0 || xx >= n || yy < 0 || yy >= m || b[xx][yy] || !grid[xx][yy]) continue;
                            b[xx][yy] = true;
                            q.push({xx, yy}); //只有"1"才能进队列
                        }
                    }
                }
                maxn = max(maxn, tmp);
            }
        }

        return maxn;
    }
};

例二、地牢大师

链接：https://www.acwing.com/problem/content/1098/

题目

你现在被困在一个三维地牢中，需要找到最快脱离的出路！

地牢由若干个单位立方体组成，其中部分不含岩石障碍可以直接通过，部分包含岩石障碍无法通过。

向北，向南，向东，向西，向上或向下移动一个单元距离均需要一分钟。

你不能沿对角线移动，迷宫边界都是坚硬的岩石，你不能走出边界范围。

请问，你有可能逃脱吗？

如果可以，需要多长时间？

输入格式

输入包含多组测试数据。

每组数据第一行包含三个整数 L,R,C

分别表示地牢层数，以及每一层地牢的行数和列数。

接下来是 L个 R 行 C 列的字符矩阵，用来表示每一层地牢的具体状况。

每个字符用来描述一个地牢单元的具体状况。

其中, 充满岩石障碍的单元格用”#”表示，不含障碍的空单元格用”.”表示，你的起始位置用”S”表示，终点用”E”表示。

每一个字符矩阵后面都会包含一个空行。

当输入一行为”0 0 0”时，表示输入终止。

输出格式

每组数据输出一个结果，每个结果占一行。

如果能够逃脱地牢，则输出”Escaped in x minute(s).”，其中X为逃脱所需最短时间。

如果不能逃脱地牢，则输出”Trapped!”。

数据范围

1≤L,R,C≤100

输入样例：

3 4 5
S....
.###.
.##..
###.#

#####
#####
##.##
##...

#####
#####
#.###
####E

1 3 3
S##
#E#
###

0 0 0

输出样例：

Escaped in 11 minute(s).
Trapped!

题目分析

起点和终点已定；方向确定；带有强烈的步数暗示。

和常规的bfs搜索方向不同，此题的搜索方向由二维变成三维。其它一样。

参考代码（带注释）

#include <bits/stdc++.h>
#define x first
#define y second

using namespace std;
int h, n, m;
const int N = 105;
char a[N][N][N];
bool b[N][N][N];
//搜索方向 六个
int dx[6] = {0,0,1,-1,0,0}; int dy[6] = {-1,1,0,0,0,0}; int dz[6] = {0,0,0,0,1,-1}; 
int st[3], en[3];

//要注意存储下标的意义
void solve()
{
    memset(b, 0, sizeof b);
    for(int i = 0; i < h; ++ i) for(int j = 0; j < n; ++ j) for(int k = 0; k < m; ++ k) //z x y
    {
        cin >> a[i][j][k];
        if(a[i][j][k] == 'S') st[2] = i, st[0] = j, st[1] = k, b[j][k][i] = true;
        else if(a[i][j][k] == 'E') en[2] = i, en[0] = j, en[1] = k;
        else if(a[i][j][k] == '#') b[j][k][i] = true;
    }
    queue<pair<pair<int, int>, int>>q;
    q.push({{st[0], st[1]}, st[2]}); //x y z
    int step = 0; bool flag = false;
    //常规bfs 只是换了下搜索方向
    while(q.size())
    {
        int len = q.size();
        step ++; //题目特性：记录时间 所以必须要每次拟清空队列
        while(len --)
        {
            auto it = q.front(); q.pop();
            int x = it.x.x, y = it.x.y, z = it.y;
            for(int i = 0; i < 6; ++ i)
            {
                int xx = x + dx[i], yy = y + dy[i], zz = z + dz[i];
                if(xx < 0 || xx >= n || yy < 0 || yy >= m || zz < 0 || zz >= h || b[xx][yy][zz]) continue;
                if(xx == en[0] && yy == en[1] && zz == en[2]) 
                {
                    flag = true;
                    break;
                }
                b[xx][yy][zz] = 1;
                q.push({{xx, yy}, zz});
            }
            if(flag) break;
        }
        if(flag) break;
    }
    if(flag) printf("Escaped in %d minute(s).\n", step);
    else puts("Trapped!");
}

int main()
{
    while(cin >> h >> n >> m && h) solve();
    return 0;
}

二、多源

与单源的区别

什么情况下用多源同时遍历？某些点有共同的特性以至于要从这些点同时开始

例题 腐烂的橘子

链接：https://leetcode-cn.com/problems/rotting-oranges

题目

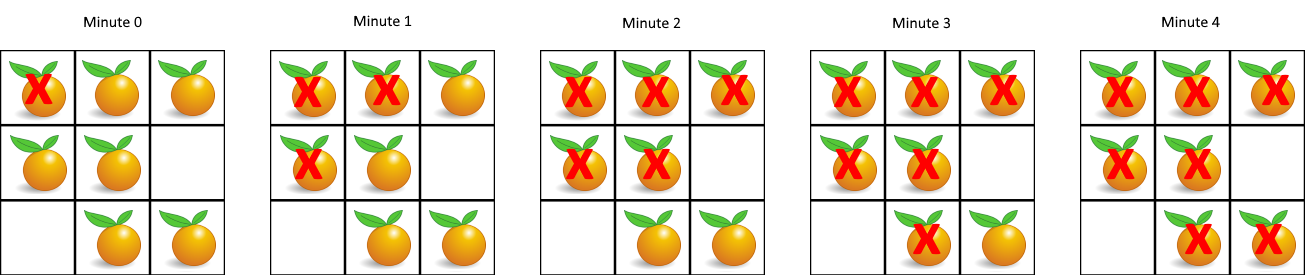
在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

值 0 代表空单元格；
值 1 代表新鲜橘子；
值 2 代表腐烂的橘子。

每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。

返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

示例 1：

输入：grid = [[2,1,1],[1,1,0],[0,1,1]]
输出：4

示例 2：

输入：grid = [[2,1,1],[0,1,1],[1,0,1]]
输出：-1
解释：左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个正向上。

示例 3：

输入：grid = [[0,2]]
输出：0
解释：因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 10
grid[i][j] 仅为 0、1 或 2

题目分析

和“时间”挂钩；多个腐烂的橘子同时向四周腐烂。

常规的bfs基础上多点同时开始即可

参考代码（带注释）

class Solution {
public:
    int dx[4] = {0, 0, 1, -1}; int dy[4] = {1, -1, 0, 0};
    int orangesRotting(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();
        vector<vector<bool>>b(n, vector<bool>(m));
        int count = 0, sum = 0, zi = 0;
        queue<pair<int, int>>q;
        for(int i = 0; i < n; ++i){
            for(int j = 0; j < m; ++j){
                if(grid[i][j] == 2){
                    b[i][j] = true;
                    q.push({i, j});
                    ++zi;
                }
                else if(grid[i][j] == 1)
                    ++sum;
            }
        }
        if(sum + zi == 0) return 0; //没有橘子

        int step = -1;
        while(!q.empty()){
            step ++;
            int len = q.size();
            while(len --)
            {
                auto [x, y] = q.front(); q.pop();
                for(int i = 0; i < 4; ++ i)
                {
                    int xx = x + dx[i], yy = y + dy[i];
                    if(xx < 0 || xx >= n || yy < 0 || yy >= m || b[xx][yy] || !grid[xx][yy]) continue;
                    count ++;
                    b[xx][yy] = true;
                    q.push({xx, yy});
                }
            }
        }
        return (count == sum) ? step : -1;
    }
};

总结

模板会了后和二维矩阵相关的裸题很简单，但有时候就是看不出来题目在考哪个知识点。

以上是蒟蒻写的简单bfs。希望能帮助到萌新，欢迎菊苣们指正。